
编辑评论:
独家笔记整理,高斯课堂高分系统学习配套讲座免费分享,需要备考的玩家可以对比学习,大大减少整理和处理时间,一套非常完整的讲义,标注了重点,方便阅读。
 >
>
高斯课堂高等数学pdf图片预览




课程目录介绍
多元函数和重限制
偏导数和全导数
复合函数和隐式函数
梯度、方向导数、多元函数极值
向量与空间几何(一)
向量与空间几何(二)
二重积分—笛卡尔坐标系
二重积分—极坐标系
三重积分
第一类曲线积分
第二类曲线积分
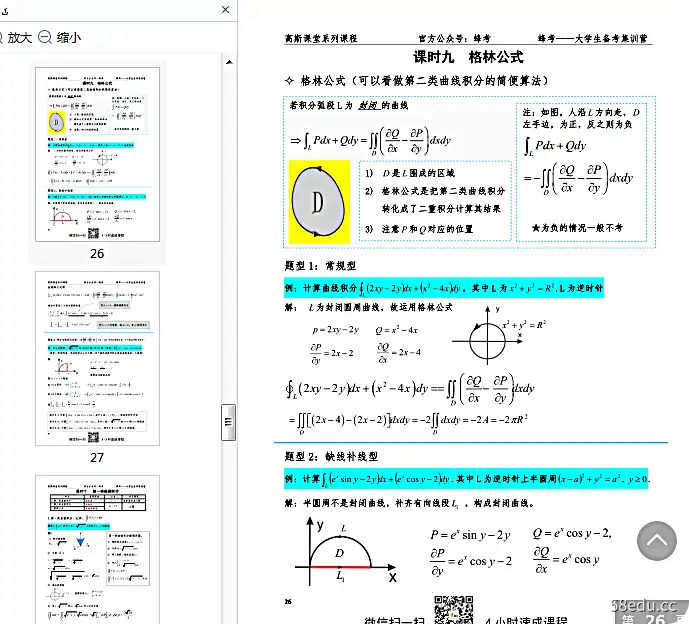
格林公式
第一类曲面积分
第二类曲面积分
高斯公式
常数项序列
电源系列
高等数学下的知识点总结与分享
首先我们了解了空间解析几何。平面的三个方程适用于不同类型的问题:


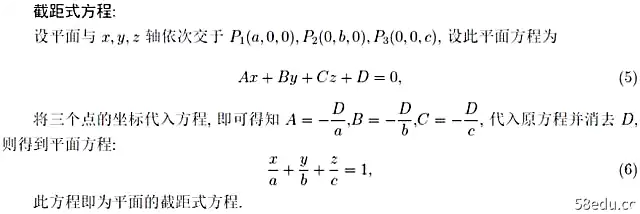
类比平面解析几何,不难得出以下角度和距离的概念:


研究完平面,我们来研究直线。直线也有以下三个方程:
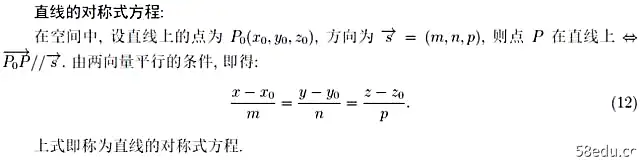

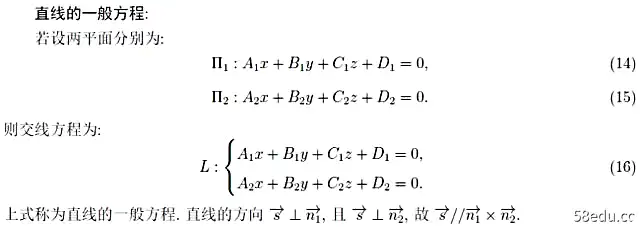
夹角的计算方法如下:


使用比直线更好的平面光束可以解决很多问题:
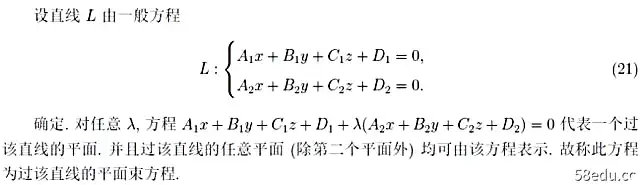
在研究了直线之后,我们研究了曲线。该曲线具有以下形式的一般方程:

曲线也可以用参数方程表示:

我们也有投影的概念:

空间解析几何的研究在一定程度上为多元函数的研究提供了基础。学生应牢记多元函数的最基本概念:

然后我们研究了偏导数:

以及高阶偏导数:

利用全微分的概念,你可以处理很多计算偏导数的问题:
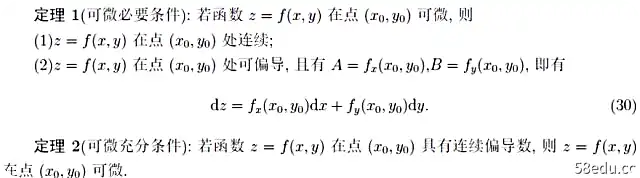
在研究了最简单的偏导数之后,我们要研究复合函数的偏导数。由于复合方法的多样性,也有以下两种不同的情况:
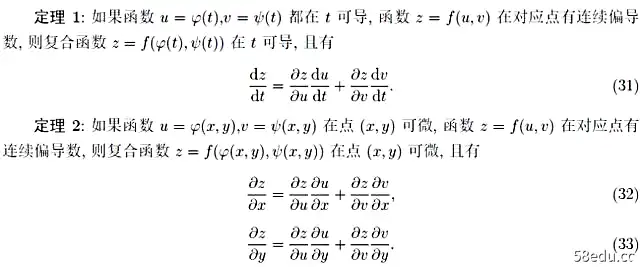
隐函数定理的结局!在方程的情况下,偏导数的计算公式如下:
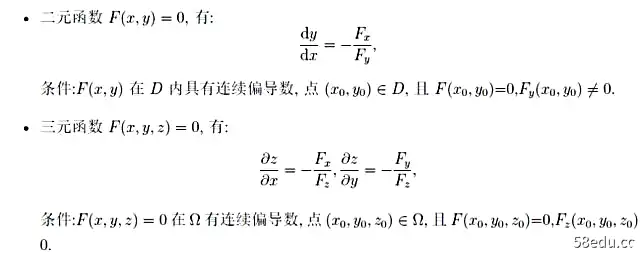
在联立方程的情况下,我们引入雅可比行列式的概念,方法如下。乍一看,这个公式似乎很复杂,但实际上是在求解一个线性方程组~

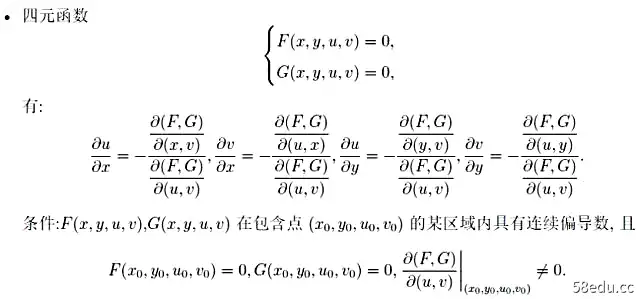
除了坐标轴方向的偏导数,我们还可以定义任意方向的方向导数。自然就用到了梯度的概念:

反过来,多元泛函微积分在第 1 章中提供了空间解析几何的方法:

没有限制,我们可以使用偏导数来求多元函数的极值:

接触过中学数学竞赛的同学会被中学数学竞赛中的小尺度和“先猜后证”搞糊涂,这里的拉格朗日乘数法让你瞬间秒杀多条件极值问题 !

上学期,学生们学习了定积分和异常积分,但是一些具体的异常积分是传统方法无法解决的。这是在我们重新融入的帮助下完成的。与定积分类比,二重积分具有以下两个性质:
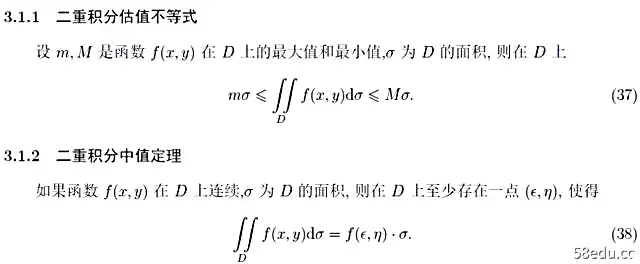
如何计算重积分可以说是高数的关键部分。一般来说,我们将积分区域分为以下两个区域,然后求解。事实上,我们仍然在做定积分。必要时,还交换积分顺序。

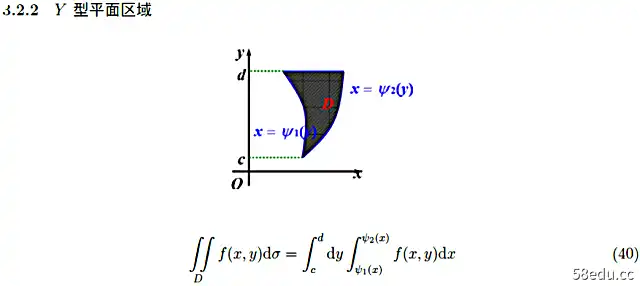
三重积分有两种基本的计算方法。我们的想法是将三重积分转换为二重积分和定积分。

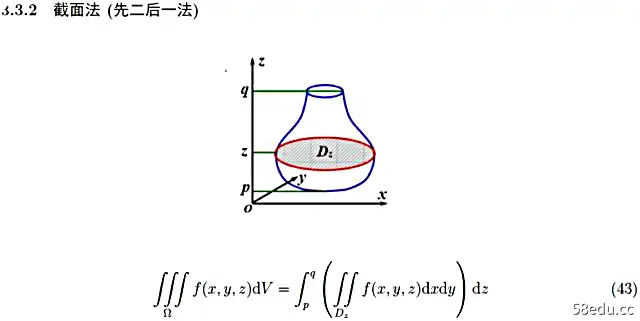
当然,有时使用对称性可以大大简化问题:

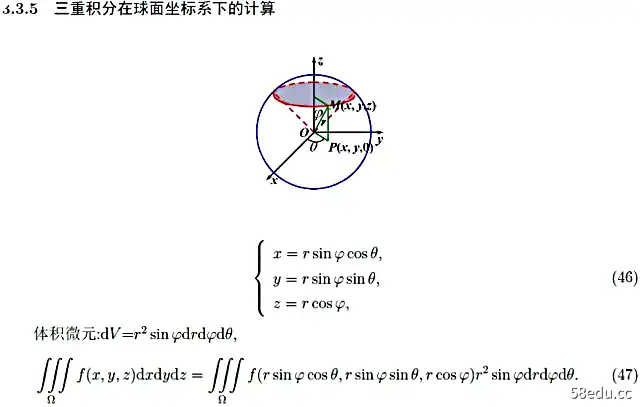
我们还介绍了柱坐标系和球坐标系,它们的体积元素可以借助雅可比行列式进行计算。这两个坐标系通常会简化问题,就像极坐标在二重积分中所做的那样。

重新整合后,我们有连线和面积点:

曲线积分的一般方法如下:
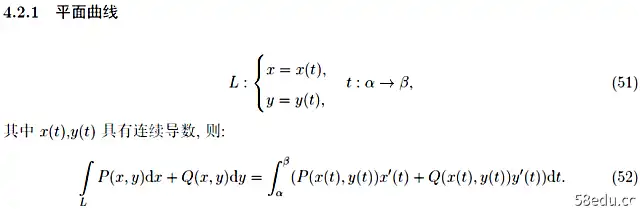

表面积分的一般方法如下:
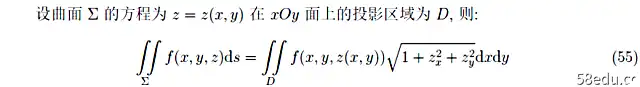
接下来是本章最重要的公式之一——格林公式及其推论:
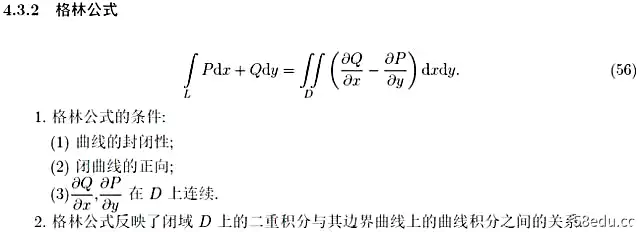

也是最重要的公式之一——高斯公式:

学期末学习了级数理论,需要牢记收敛法~

我们讨论了两个重要的函数项级数——幂级数和傅里叶级数。其实同学们在学习泰勒公式的时候就已经接触到幂级数了~而傅里叶级数,用三角级数拟合一般周期函数,是一个非常棒的想法。傅里叶级数的公式有点复杂,请记住公式和结论,不要混淆~


声明:本站所有资源版权均属于原作者所有,这里所提供资源均只能用于参考学习用,请勿直接商用。若由于商用引起版权纠纷,一切责任均由使用者承担。如若本站内容侵犯了原着者的合法权益,可联系我们进行处理。














暂无评论内容